欢迎光临广西法制网！
今天是 2024年12月27日 星期五
关注社会热点
一起实现我们的中国梦
关注社会热点
一起实现我们的中国梦
韦东奕：太简单了，没必要要钱。
基础科学领域的研究总是让人感到晦涩难懂，但我们常常能从一些「小事」上看出其中意义。
5 月 6 日，一张微信聊天截图，将北大助理教授韦东奕再次送上了热搜：
图片来源：微博 @贼叉据这张截图介绍，一家科技公司使用 PS5 做了一个集群用来模拟产品的物理性能，但随着模型越复杂，模拟失真就越高。包含六位博士在内的团队花了四个多月未能解决，团队猜测是因为「对纳维斯托克斯方程的处理有问题」，但是又搞不清楚哪里有问题。
后来，他们向韦东奕寻求了帮助。韦东奕把全部方程发过来后，团队花了一天调试就成功了，并且和过往的真实实验数据匹配率高达 99.8%。
故事的结尾是：韦东奕拒收报酬，表示「太简单了，没必要要钱」，最终这家公司给韦东奕充了市政公交一卡通……
听完这个过程，有网友表示：「这结局太魔幻了，有种在看网络爽文的感觉。」
朴实无华韦东奕
韦东奕最初的无意间「走红」，也是由于一次热搜。
2021 年 5 月，有媒体探访北大校园时，采访到了韦东奕。在采访视频中，韦东奕手持 1.5L 装矿泉水瓶，拎着两个用塑料袋打包的馒头，其质朴形象一度引发热议，人称「韦神」、「北大数学系扫地僧」。
韦东奕 2007 年升入山东师范大学附属中学。高一时参加第 49 届国际数学奥林匹克竞赛（IMO），以满分获获得金牌。2009 年，高二时韦东奕参加第 50 届国际数学奥林匹克竞赛，再次满分夺金。
2010 年，韦东奕被保送至北京大学就读；2014 年本科毕业后在北京大学硕博连读；2018 年博士毕业后在北京国际数学研究中心从事博士后研究工作；2019 年被聘为北京大学助理教授。他的博士论文《轴对称 Navier-Stokes 方程与无粘阻尼问题》，被评为北京大学 2018 年优秀博士学位论文。
相传哈佛大学为招徕韦东奕，曾提出可以为其破格免掉英语考试，但被后者拒绝。韦东奕自称「不喜欢出远门，尤其在疫情期间，如果一些学术会议可以线上参加，那我就线上参加」。平时除了做数学，他喜欢听收音机里的新闻和评论， 每天关注卫健委公布的新冠确诊人数。
目前，韦东奕的数学研究领域主要聚焦于分析、偏微分方程和随机矩阵等。
2021 年，韦东奕获得达摩院青橙奖时，其答辩主题就是有关湍流问题和流动稳定性问题，他提出的两个原创性的数学方法解决了流动稳定性领域一系列重要的公开问题。
物理学家费曼曾经说过，湍流可能是经典物理学中最后的一个未解难题。
NS 方程：流体力学基石
流体力学的数值模拟对于建模多种物理现象而言非常重要，如天气、气候、空气动力学和等离子体物理学。通常，流体可以用纳维 - 斯托克斯方程（Navier-Stokes equations，NS）来描述，但大规模求解这类方程仍属难题，受限于解决最小时空特征的计算成本。
它由法国工程师、物理学家克劳德 - 路易 · 纳维，爱尔兰物理学、数学家乔治 · 斯托克斯两人命名，是一组偏微分方程，表达了牛顿流体运动时动量和质量的守恒。
该方程断言，流体粒子动量的改变率（力）来自作用在液体内部的压力变化、耗散粘滞力、以及重力。其中粘滞力类似于摩擦力，产生于分子的相互作用，越黏的流体，该作用就越强。
NS 方程依赖微分方程来描述流体的运动。不同于代数方程，其不寻求建立所研究的变量（如速度和压力）的关系，而是寻求建立这些量的变化率或通量之间的关系。用数学术语来讲，这些变化率对应于变量的导数。其中，在零粘滞度的最简单情况下，NS 方程化为欧拉方程，表明加速度（速度的导数）与内部压力的导数成正比。
这表示对于给定的物理问题，至少要用微积分才可以求得其纳维 - 斯托克斯方程的解。实用上，也只有最简单的情况才能用这种方法获得已知解。这些情况通常涉及稳定态（流场不随时间变化）的非紊流，其中流体的粘滞系数很大或者其速度很小（低雷诺数）。
对于更复杂的情形，例如厄尔尼诺现象这样的全球性气象系统或机翼的升力，现时仅能借助计算机求出纳维 - 斯托克斯方程的数值解。该科学领域被称为计算流体力学。
它是一个混沌模型，当输入存在一点点不准确，预测结果就会大相径庭。
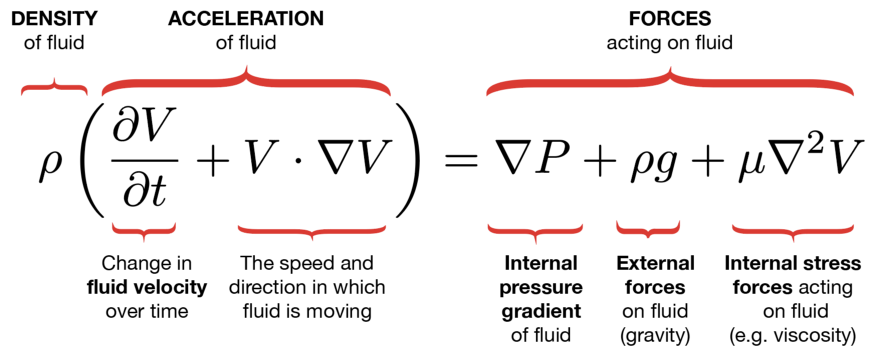不可压缩流体通常由如上纳维 - 斯托克斯方程来建模。由于其重要性，「纳维 - 斯托克斯存在性与光滑性」被美国克雷数学研究所在 2000 年列为七大千禧年大奖难题之一，解题奖金 100 万美元。与它并列的其他问题包括庞加莱猜想、P/NP 问题、霍奇猜想、黎曼猜想、杨 - 米尔斯理论、贝赫和斯维讷通 - 戴尔猜想，至今只有庞加莱猜想已获解决。
回到本次事件，北大数学学院院长在媒体回复中表示，此事有人发给他看过。他表示：「别人做不出来，韦东奕能做出来是很平常的事。第一，韦东奕人很聪明。第二，他很专心做数学。他就是生活方式比较淳朴，我们尊重他的意愿。」
另外，由于消息来源只有一张聊天截图，这一事件的真实性也引发了部分质疑：
你怎么看？
韦东奕数学北京大学
